Ontario scientist helps discover new shape, solve decades-old math problem
 Craig Kaplan, an associate professor in computer science at the University of Waterloo, with two "einsteins" (Credit: University of Waterloo).
Craig Kaplan, an associate professor in computer science at the University of Waterloo, with two "einsteins" (Credit: University of Waterloo).
An Ontario scientist helped discover an “einstein” – a longstanding mathematical problem deemed impossible for more than 60 years – until now.
An “einstein” is a formation of shapes that perfectly interlocks with one another, without gaps or overlaps, just like the bricks that assemble a house. In an einstein, however, the pattern of shapes never repeats.
Until this month, scientists had yet to discover a shape that could create such a pattern.
“The problem we were trying to solve was whether there is a single shape that had this property,” Craig Kaplan, an associate professor in computer science at the University of Waterloo, told CTV News Toronto.
In the math community, this concept is referred to as an “aperiodic monotile,” also the name of a research paper co-authored by Kaplan earlier this month.
“What we found is a single shape that can never make periodic tilings.”
That shape turned out to be what Kaplan and his colleagues have called “the hat” – tied to its resemblance of a fedora. Visually, it resembles eight kites glued together to make a single 13-sided shape.
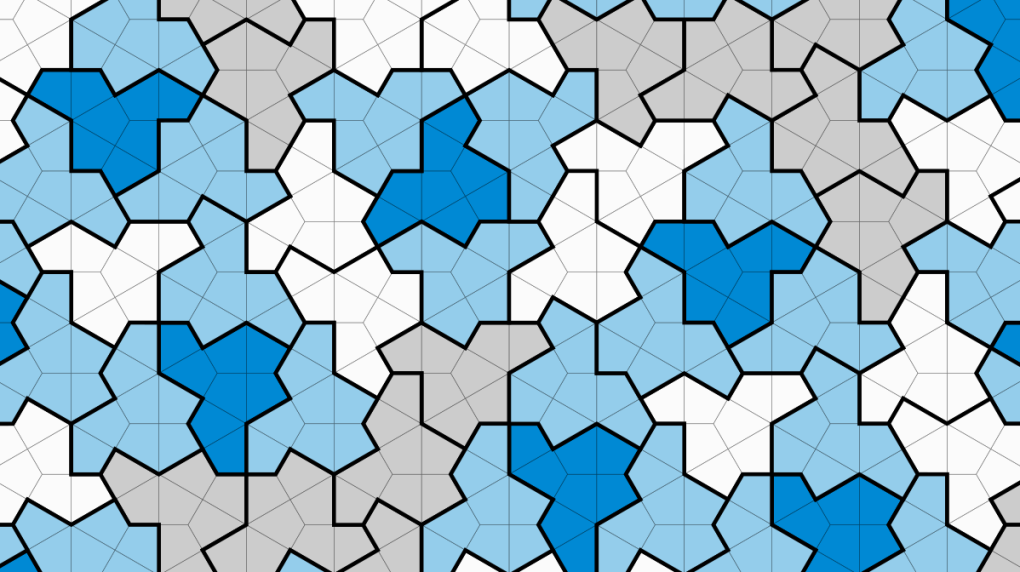 A tile formation of shapes that perfectly interlock with one another and never repeat (Craig Kaplan). The longstanding belief that an “aperiodic monotile” could not exist was put forward by mathematician Hao Wang in 1961.
A tile formation of shapes that perfectly interlock with one another and never repeat (Craig Kaplan). The longstanding belief that an “aperiodic monotile” could not exist was put forward by mathematician Hao Wang in 1961.
Soon after, one of Wang’s students discovered an aperiodic set of 20,426 tiles, and then, a set of 104. In the 1970s, mathematical physicist and Nobel Prize winner Roger Penrose reduced that number down to two.
But over the last several decades, progress hit a standstill.
'PROFOUND DISCOVERY'
Kaplan became aware of the existence of "the hat" after receiving an email last November "out of the blue" from David Smith, a retired printing technician in England.
“He emailed me and asked if the work I had done previously might be useful in trying to understand its properties,” Kaplan recalled.
Smith was interested in software Kaplan had previously crafted that had the capability to automate a visualization of hundreds of hats glued together. Smith wanted to use Kaplan's software to find out if this shape could solve the longstanding problem.
Until this point, Smith had been physically cutting his newfound shape out of cardstock, a pursuit he chronicled in his personal blog, to see if his “hat” could in fact solve the unsolvable.
Within just five months of connecting, Smith, Kaplan and two others, Chaim Goodman-Strauss and Joseph Myers, published a research paper on the previously impossible “aperiodic monotile” in Cornell University’s archive while awaiting a peer-review.
“It settles a longstanding open problem in mathematics,” Kaplan said.
“That sense of discovery is profound.”
CTVNews.ca Top Stories

DEVELOPING Driver rams New Year's revellers in New Orleans, killing 10. FBI investigating as 'act of terrorism'
A driver brought carnage on New Orleans' famed French Quarter early on New Year's Day, ramming a pickup truck into a crowd and killing 10 people before being shot to death by police, authorities said.
Missing hiker with arrest warrant found after friends delay police report: B.C. RCMP
Mounties in British Columbia are warning the public to be honest after a missing hiker's friends delayed reporting her disappearance to police.
Here are some of the new laws and rules coming into effect in Canada in 2025
From boosting child and disability benefits to increasing protections for workers, here’s a look at new measures coming into effect in 2025.
Financial changes in Canada you should know about this year
There are a few changes in federal policies that could affect Canadians' finances in the new year.
Ford, Acura, Land Rover recall vehicles over safety risks
Certain Ford, Acura and Land Rover models have been recalled in Canada over a variety of issues that pose a risk to drivers’ safety.
A single cigarette slashes 20 minutes off your life expectancy, U.K. research suggests
If you're thinking about making a New Year's resolution to quit smoking, it might help to know that new research says it could extend your life expectancy.
Ukraine halts transit of Russian gas to Europe after a prewar deal expired
Ukraine on Wednesday halted Russian gas supplies to European customers that pass through the country, almost three years into Moscow's all-out invasion of its neighbor, after a prewar transit deal expired at the end of last year.
FBI finds 150 homemade bombs at Virginia home in one of the largest such seizures, prosecutors say
Federal agents found one of the largest stockpiles of homemade explosives they have ever seized when they arrested a Virginia man on a firearms charge last month, according to a court filing by federal prosecutors.
'It Ends With Us' director Justin Baldoni sues New York Times for libel over Blake Lively story
'It Ends With Us' director Justin Baldoni sued The New York Times for libel on Tuesday over its story on allegations that he sexually harassed and sought to smear the reputation of the film's star, Blake Lively.
































